（一）平面介面：

折射：斯乃耳定律（Snell’s Law）

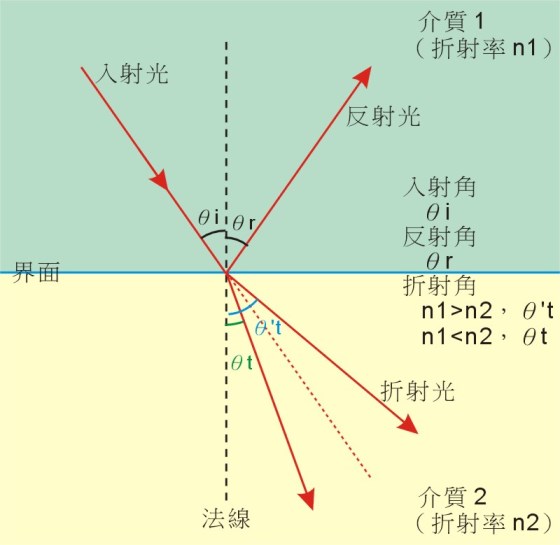
費馬原理（Fermat’s principle）：光在兩點間的光程為一極值。

利用費馬原理解釋折射現象。

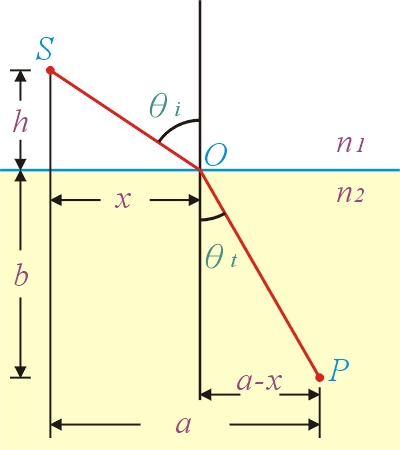
圖中，光從 S 點經過介面到達 P 點。

或

由費馬原理知道

因此

從圖中可以知道

因此

若是光通過很多層不同的介質，則

其中，，(OPL)（optical path length）光程

（二）曲面介面：

大多數透鏡為球面鏡，因此以球面介面來說明。

光源 S，經由介質 1（折射率 ）經過一球面，進入介質 2（折射率 ），聚在 P 點。此球面的球心點為 C，曲率半徑為 R。

光由介質 1 進入介質 2 有兩個路徑，一為S→V→P，另一為S→A→P。

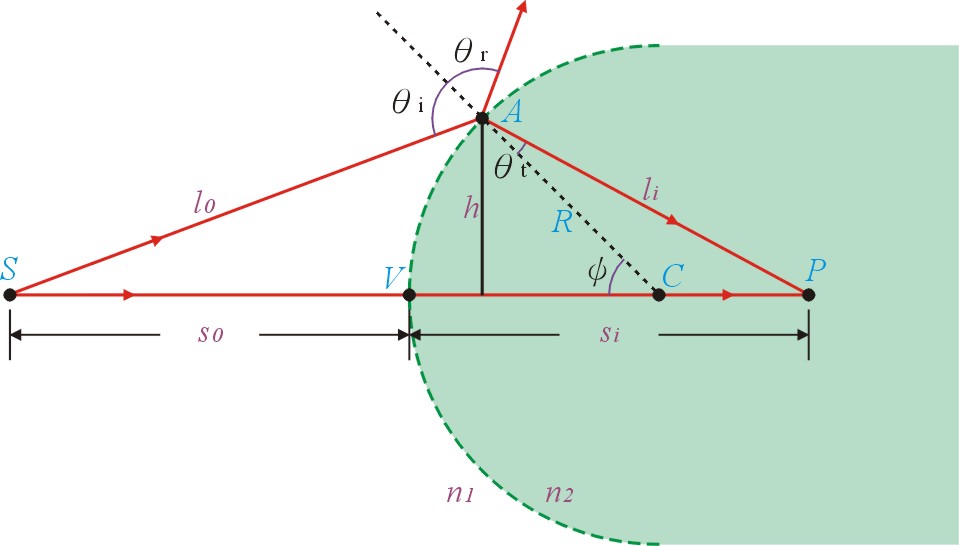
光程可寫成

圖中三角形SAC和ACP，利用餘弦定理和

可以得到

因此(OPL)可改為

光程與角度 無關

再根據費馬原理

假設 很小，A 點接近 V 點，即

且 

(i) 光通過球面後，成為平行光，即

我們定義此時的 為第一個聚焦長度（the first focal length）（物聚焦長度，the object focal length）。

(ii) 平行光通過球面後聚在一點，即

我們定義此時的 為第二個聚焦長度（the second focal length）（像聚焦長度，the image focal length）。

（三）球面薄透鏡焦距求法：

一球面薄透鏡（折射率為 ）置於折射率為 與 的介質中。

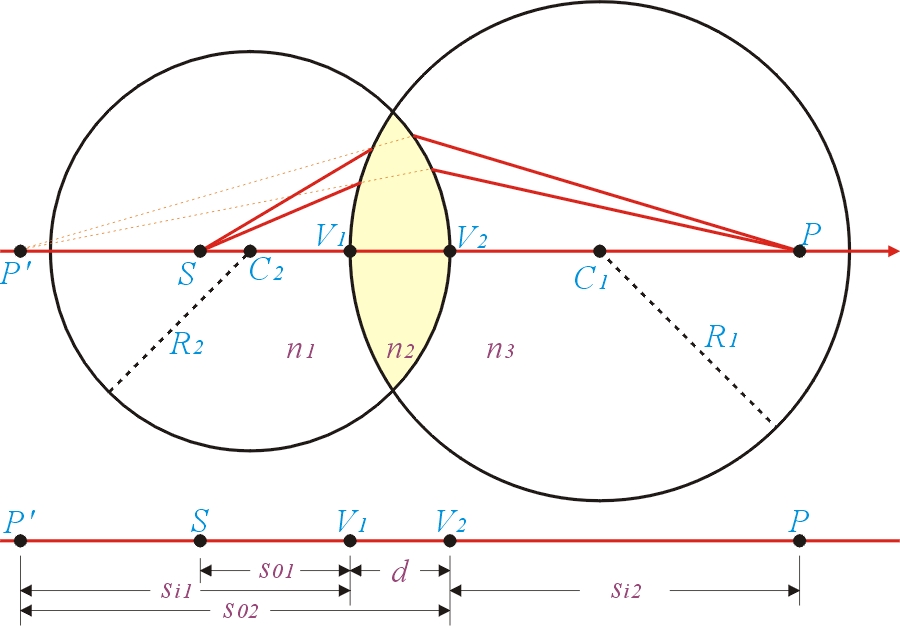
從上面的結論，，可以得到

...(1式)

...(2式)

(1式)+(2式)：

(i)

薄透鏡，因此

右焦距 ：

只討論右焦距是因為一般我們定義光從左向右傳播，我們較常需要用到右焦距。

(ii) 

透鏡大多放在空氣中，因此假設

所以 

 

 

有上兩式可以得知