
剛體(Rigid body),不因外力而型變的物體。
固定軸(Fixed axis),不變的軸,轉軸位置及指向均為固定不變。
(保齡球沿著球道的滾動rolling motion,是對一個動的軸做轉動,轉動軸一直在移動。一個圓柱沿著斜波往下滾動,轉動軸的指向不變,但轉動軸一直在移動。)
Asix of rotation (rotation axis)轉動軸,一剛體對一固定軸做轉動運動,稱此固定軸為轉動軸。
rad:radian(弧度)(徑度?弳度?...應該是弳度~不是徑度):從A點到B點,所經過的弧度大小為
弧長
半徑為R的圓的圓週長:
rev:revolution(圈)
(轉一圈= 弧度)
補充1:degree 的意思是『度數』,可用來表達『溫度』或『角度』。
在這邊,我們會稱角度為 degree,弧度為 radian。
補充2:單位弧度定義為『圓弧長度』等於『半徑』時的圓心角。
角度以弧度方式寫出來時,通常不會寫弧度單位,有時記為rad。因為圓周長為 ,所以轉一圈為弳度
,當
時,為 1 rad。

圖片來源:https://askeyphysics.org/home/
rpm=revolution per min
每分鐘轉了N圈,稱為N rpm。
一維運動與轉動運動的比較:
| 一維運動 | 轉動運動 |
=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
| 一維運動 | 轉動運動 |
| |
|
| |
|
| |
|
| |
牛二:牛頓第二運動定律
:力矩(torque)
:轉動慣量(moment of inertia)
⇒
⇒ 角速度
⇒
⇒
⇒ 角加速度
⇒
(t 指的是tangential切線方向)
(r 指的是radian向心方向)
週期:轉一圈所花的時間
頻率:每秒所轉的圈數(
)
轉動能量
I:轉動慣量(moment of inertia)
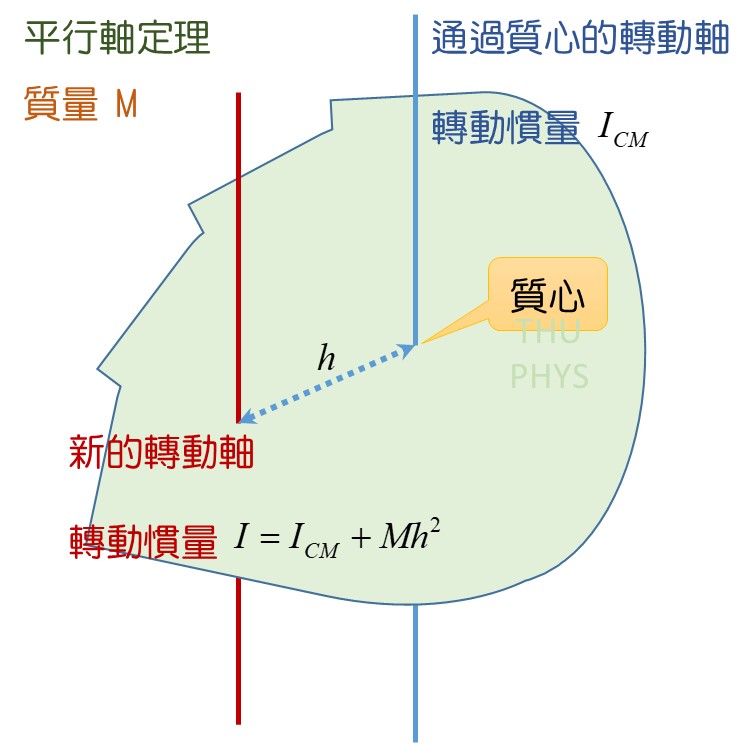
平行軸定理(parallel axis theorem)
:轉動軸通過質量中心的轉動慣量。
:新的轉動軸,與通過質心的轉動軸的距離。
一物體,其質量不會改變,但當轉軸位置不一樣時,轉動慣量就會不一樣。轉動慣量跟轉軸物與物體的距離有關。
轉動慣量(moment of inertia):
(a) 繞中心軸轉動的圓環:
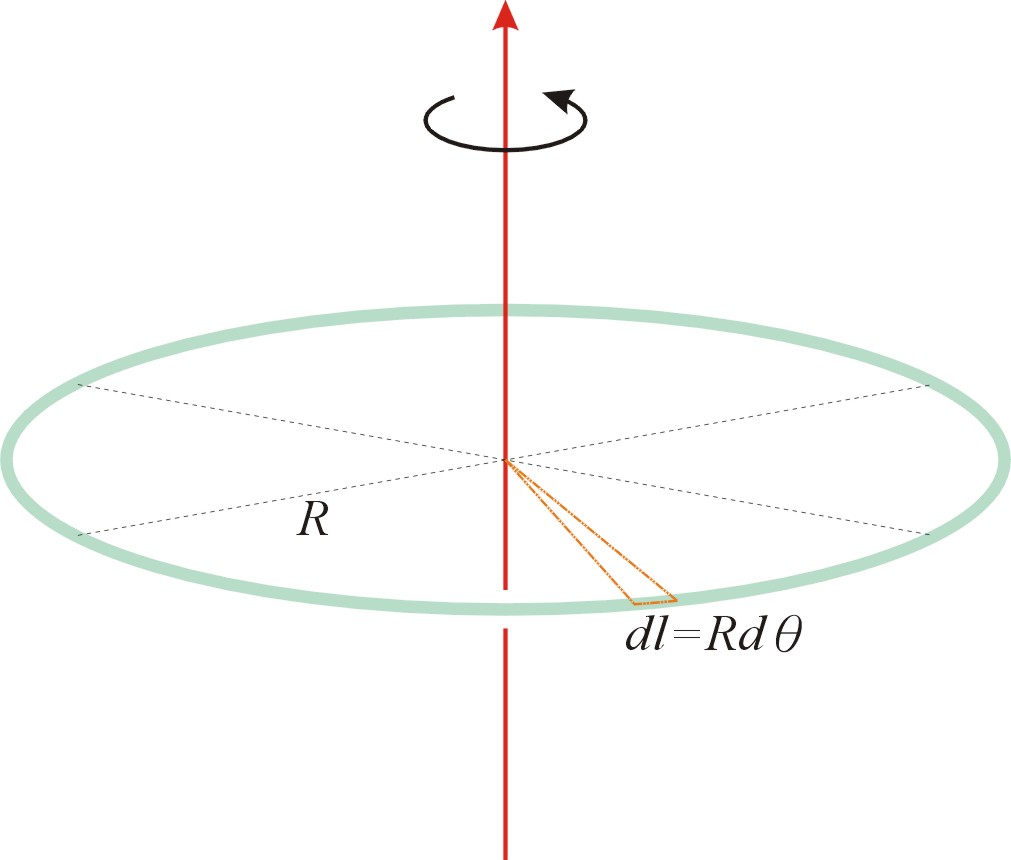
【證明】
圓環半徑
=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
(b) 繞中心軸轉動的中空圓柱(或有厚度的圓環):
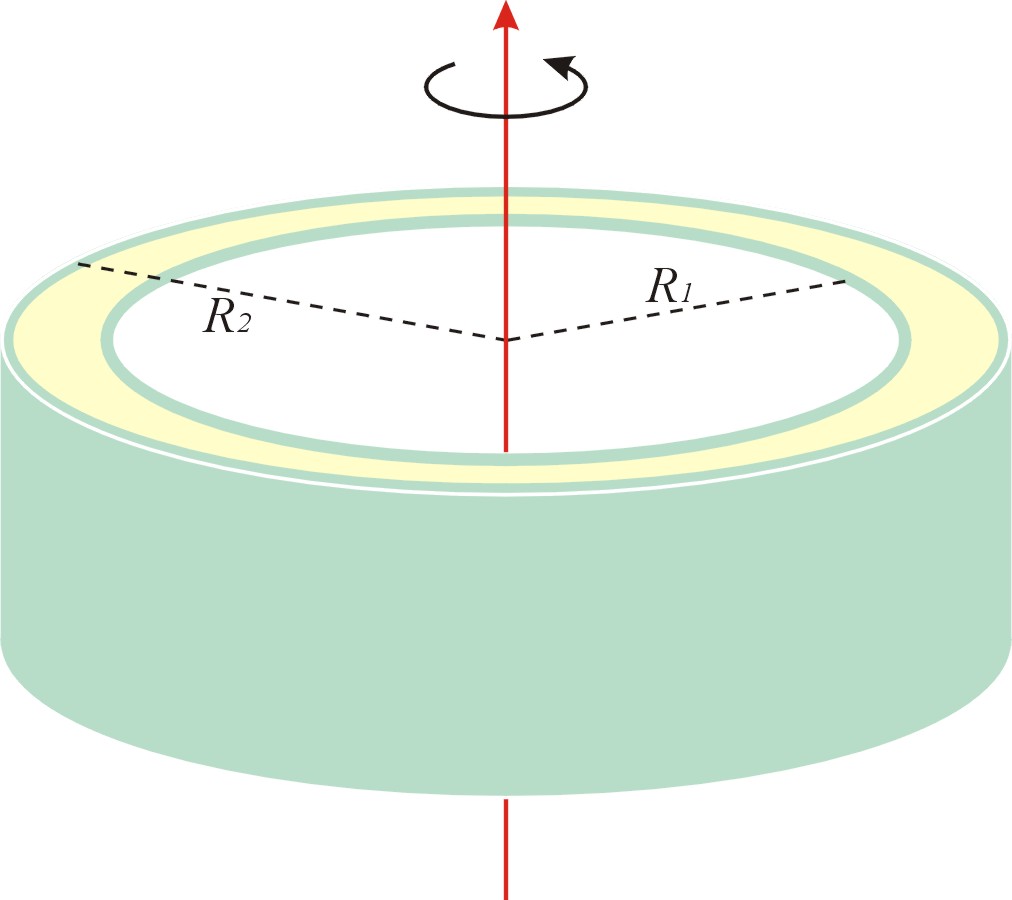
有厚度的圓環
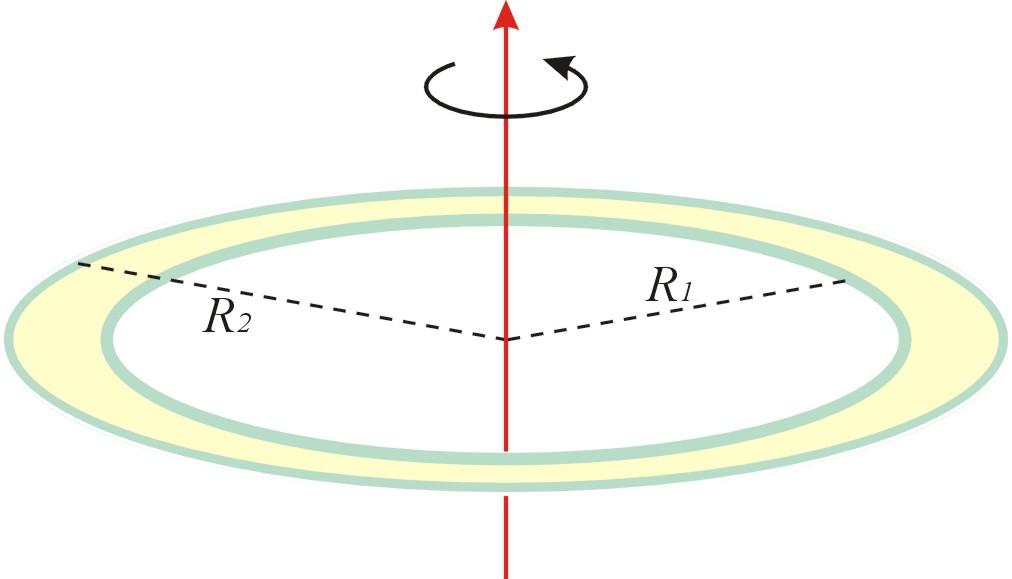
【證明】
=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
(c) 繞中心軸轉動的實心圓柱(或實心圓圓盤):
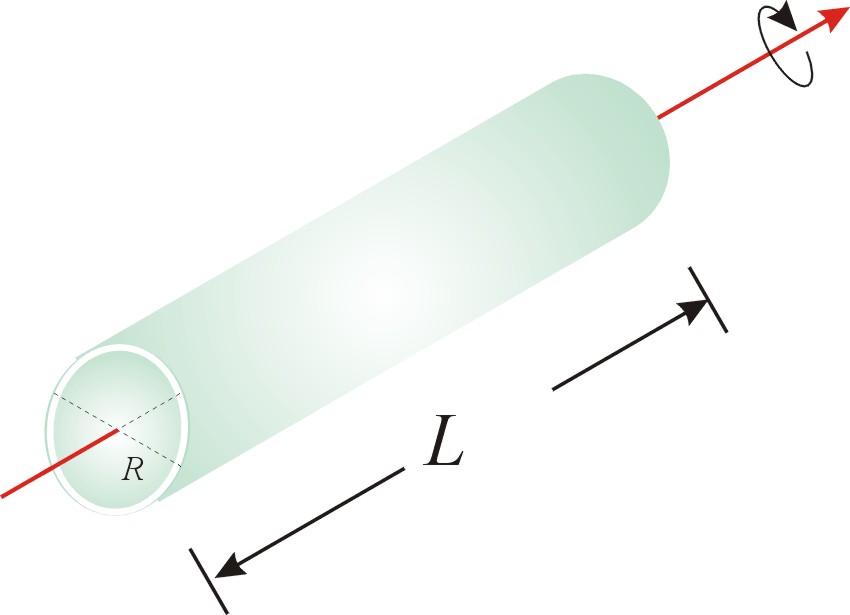
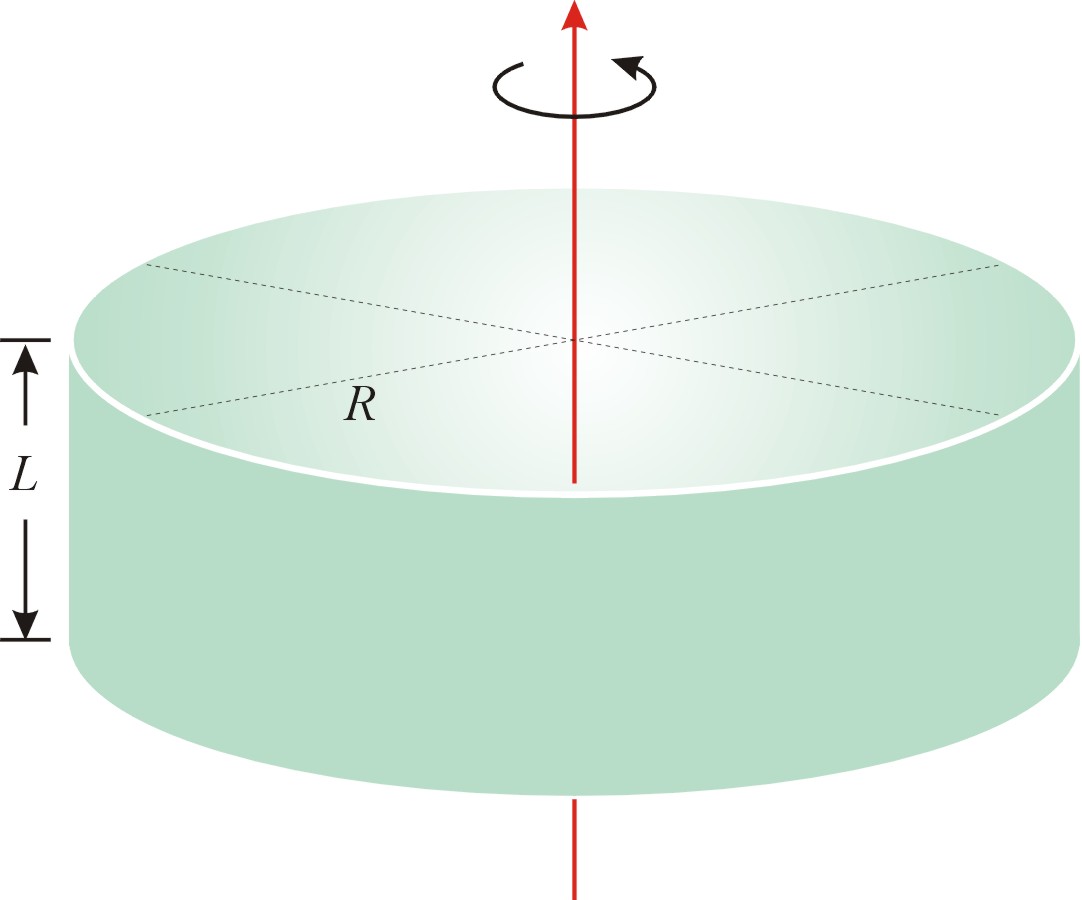
【證明】
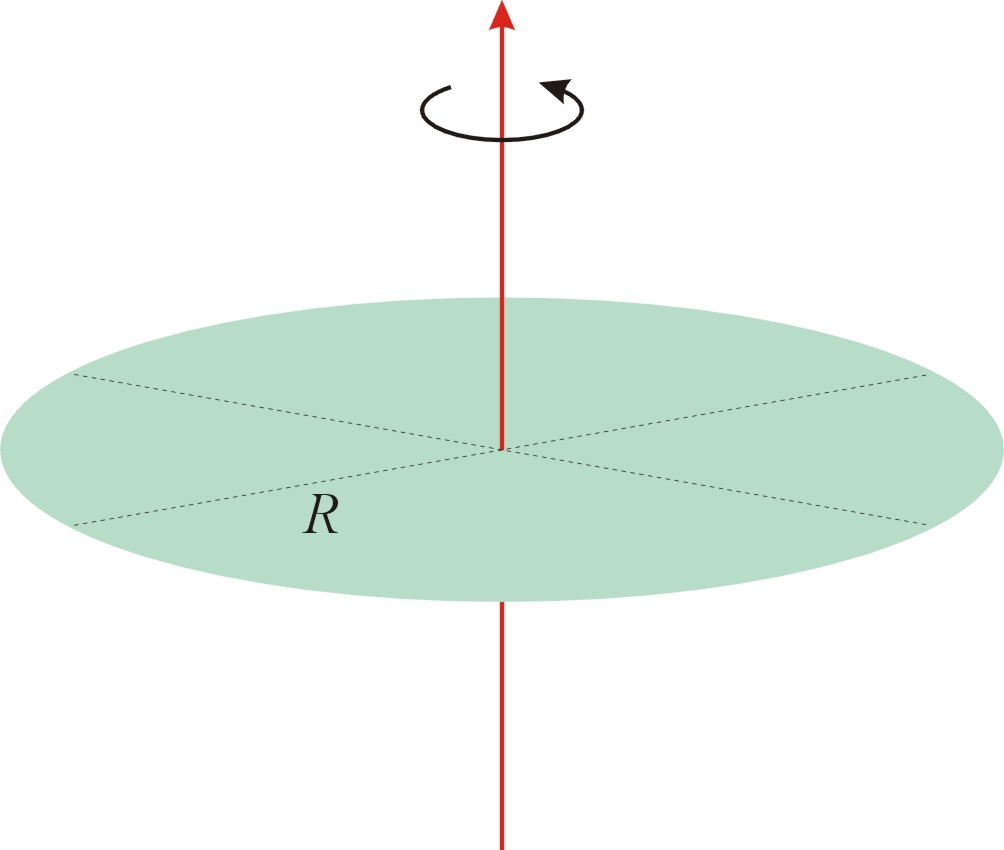
【證明】
=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
(d) 圓柱:
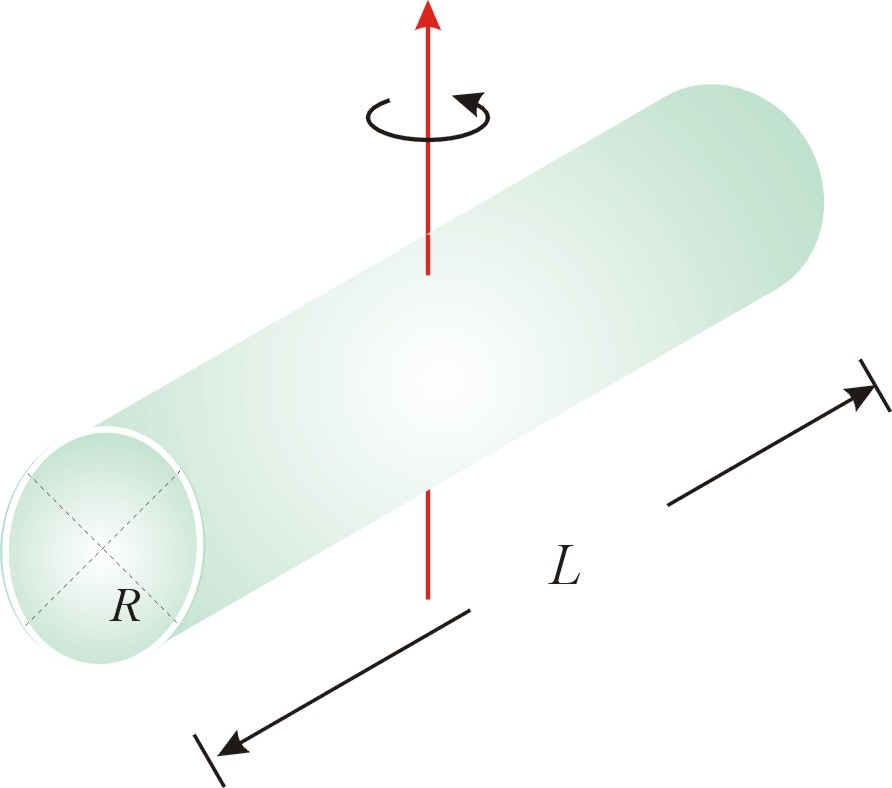
【證明】
=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
(e) 細長棒子:
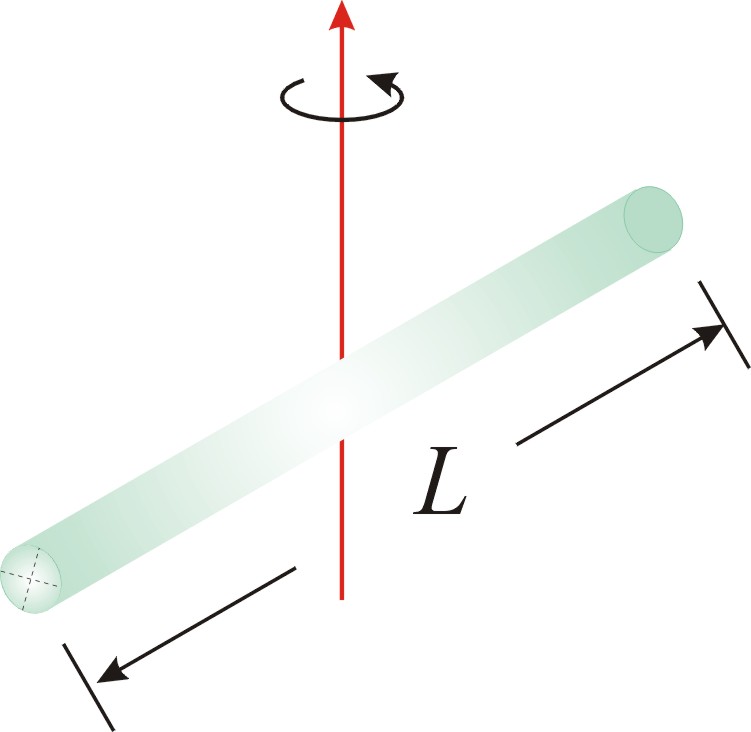
【證明】
=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
細長棒子:
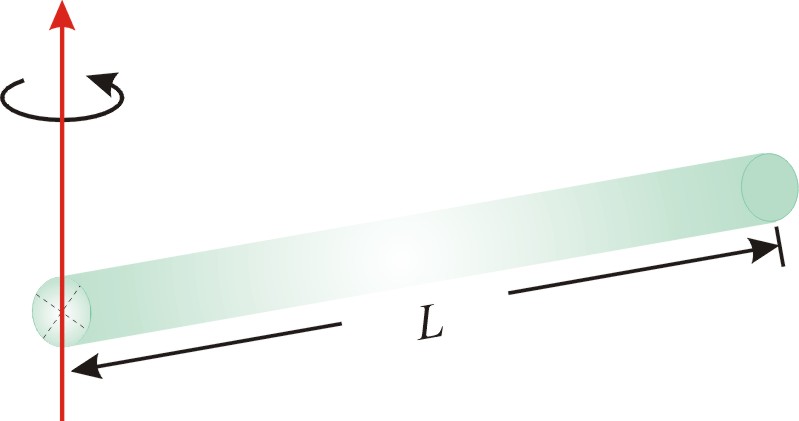
【證明】
【證明】
平行軸定理
=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
(f) 實心球體:
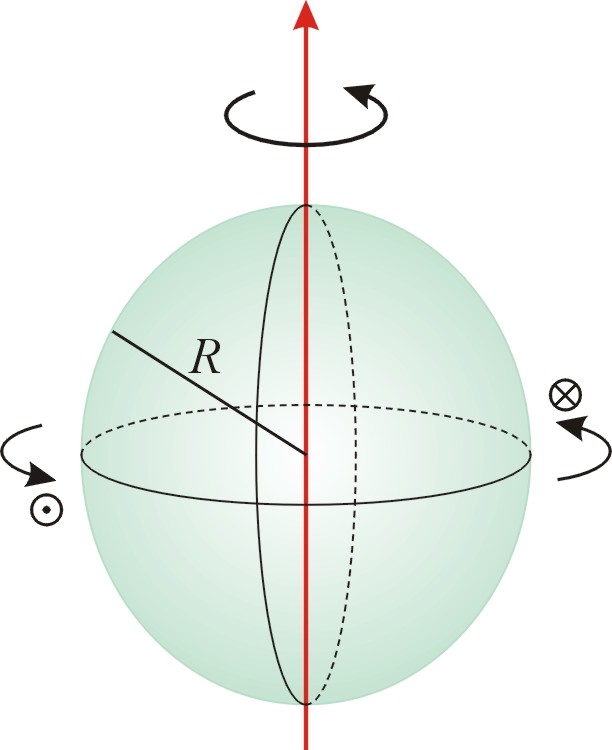
【證明】
=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
(g) 球殼:
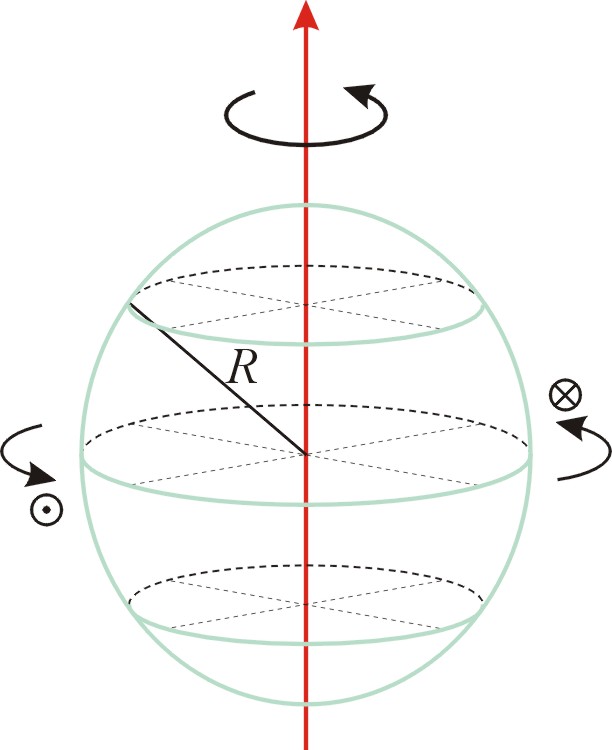
【證明】
=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
(h) 繞直徑轉動的圓環:
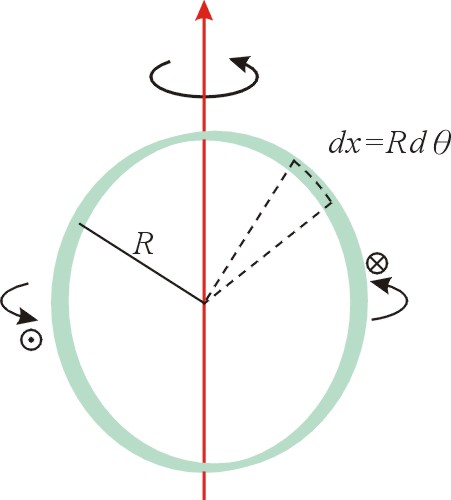
【證明】
=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
繞直徑轉動的圓盤:
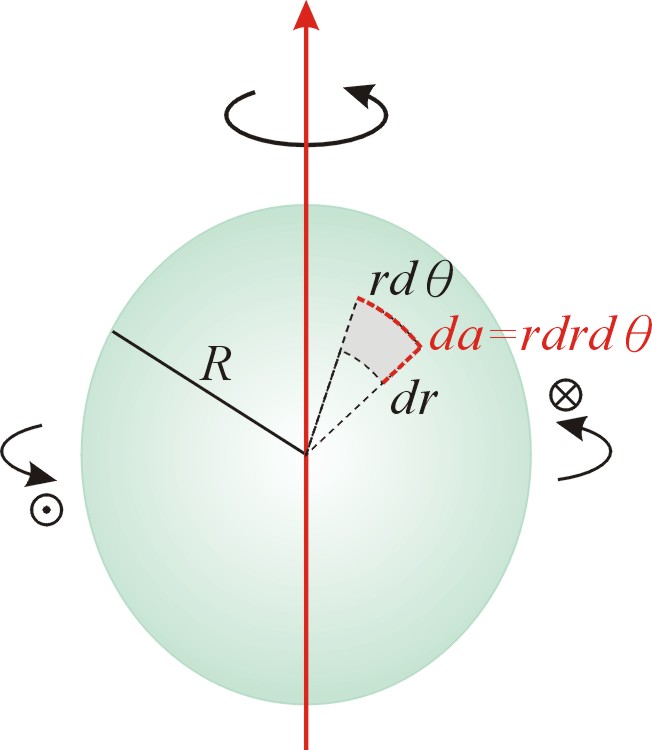
【證明】
=*=*=*=*=*=*=*=*=*=*=*=*=*=*=*=
(i) 繞通過中心垂直軸轉動的平版:
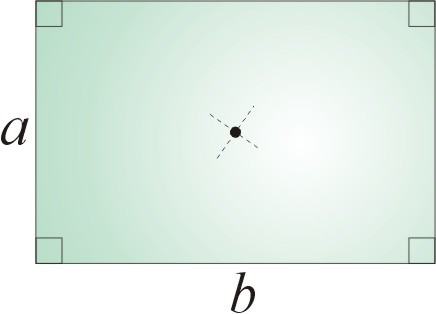
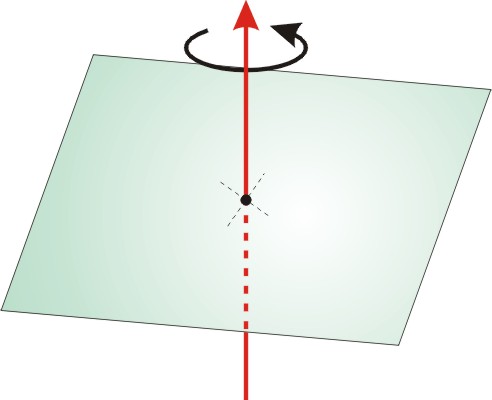
【證明】