
亞佛加厥常數(Avogadro’s Number)
Mole數:
:分子數
:質量
:莫耳質量,1莫耳的質量。
:單一個分子或原子的質量。
【補充】水分子()的『相對分子質量(分子量)』約為18.016,一莫耳水的質量為18.016克。
氫()原子量:1.008
氧()原子量:16
【補充】氫氣 與氧氣
反應生成水,可以用化學方程式表達為:
。其意義為2莫耳氫氣與1莫耳氧氣反應生成2莫耳水。
理想氣體(ideal gas)
(ideal gas law理想氣體定律)
(gas constant)
留意一下使用的單位:
==>
==>
波滋曼常數(Boltzmann constant)
(ideal gas law 理想氣體定律)
波滋曼常數
理想氣體所做的『功(Work)』:
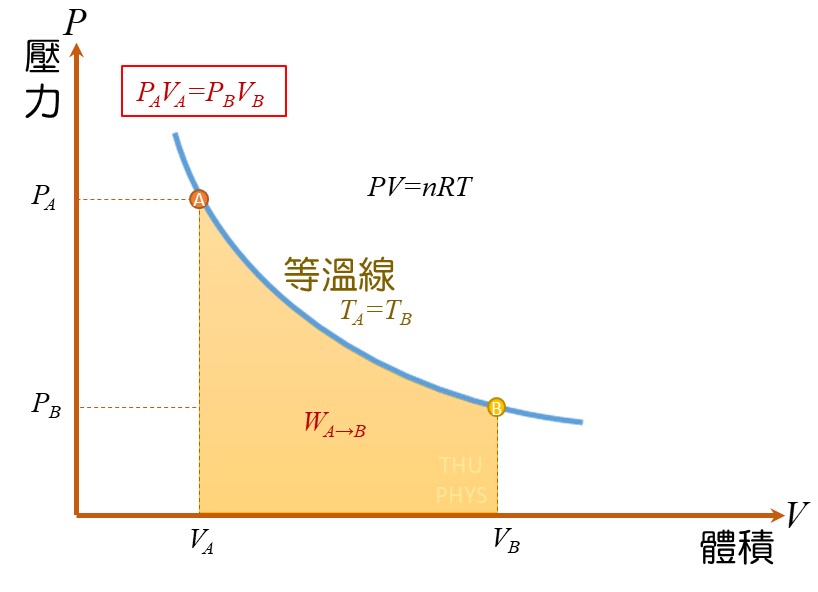
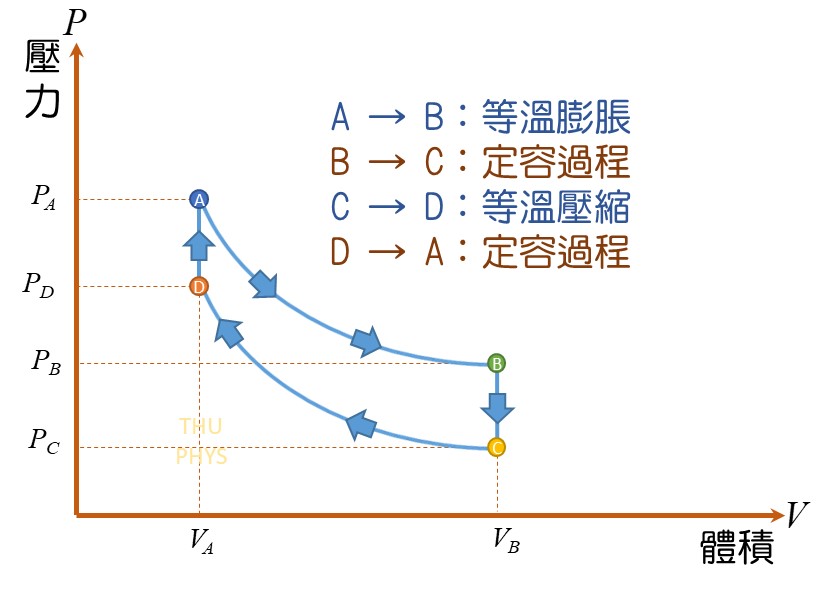
=> 等溫膨脹(isothermal constant):
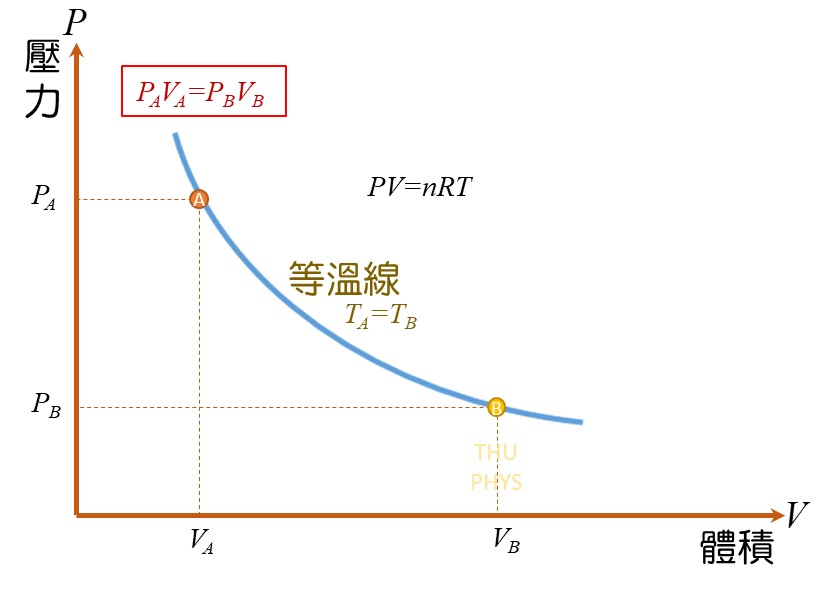
所做的功,等於等溫線底下的面積。
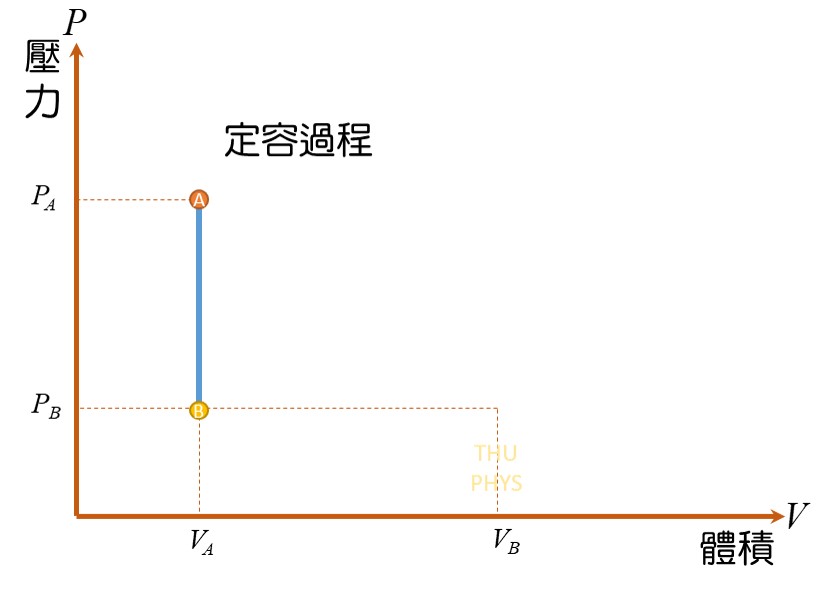
=> 定容過程(constant-volume processes):
定容,體積不變,所以不做功。
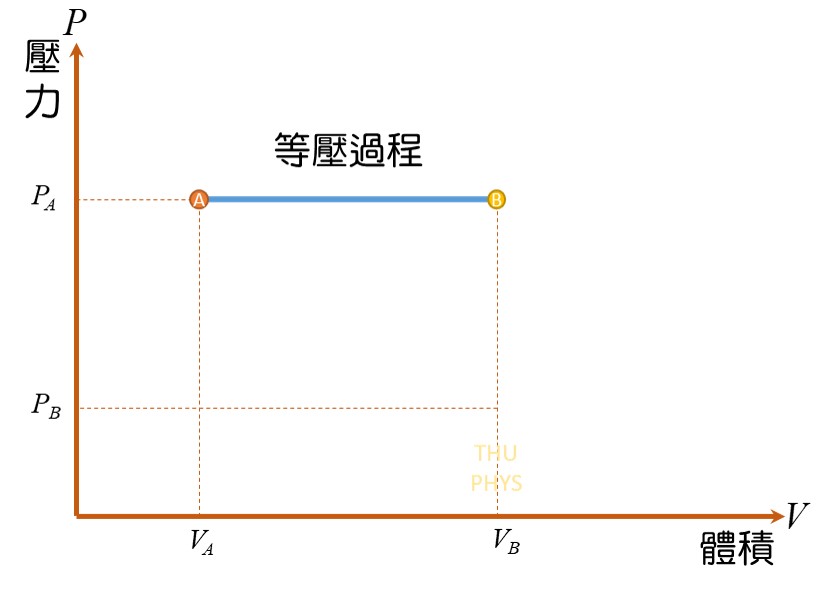
=> 等壓過程(constant-pressure processes):
將 莫耳的理想氣體密封在一個邊長為
的立方體容器內,容器壁面溫度固定為
。經過一段時間後,內部達成平衡。氣體撞擊到容器壁面的動量變化為:
(單一次撞擊)
(小寫:動量。大寫
:壓力。)
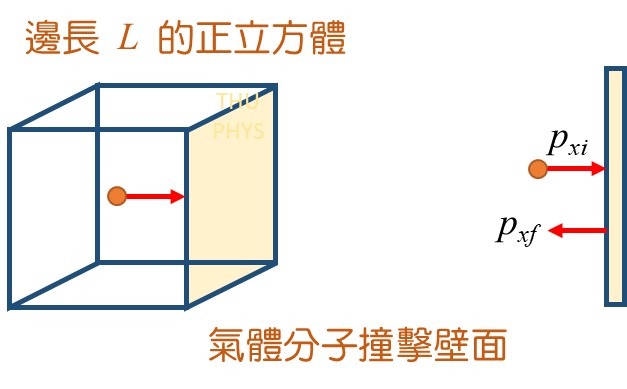
每隔 時間,氣體分子會再一次撞擊壁面。則單一分子對壁面的施力為:
分子施加在壁面的壓力為:
關於方均根(rms,root-mean-square)
先平方(square)→再平均(mean)→最後開根號(root)
平均值:
方均根值:
最可能值(眾數):,數據資料中出現次數最多的數值稱為眾數。
平移動能(Translational Kinetic Energy):
在給定溫度 之下,所有理想氣體分子,不論其質量如何,都具有相同的『平均平移動能』。
意即,當我們測量氣體的溫度時,我們還同時測量了分子的平均平移動能。
平均自由徑(mean free path):
一個分子在各次碰撞之間,所行走的平均距離。
Maxwell's speed distribution law
:機率/速率,每一個速率的機率。
平均速度
方均根速度
最可能速度(most probable speed)(眾數)
內能
:波滋曼常數(Boltzmann constant)
理想氣體的莫耳比熱(Molar specific heats)C:
:定容莫耳比熱
因為定容,體積保持不變,所以
(單原子分子氣體)
(雙原子分子氣體)
(多原子分子氣體)
=*=*=*=*=*=*=*=*=*=
:定壓莫耳比熱
定壓時所做的功:
理想氣體的莫耳比熱(Molar specific heats)C:
內能
定容莫耳比熱
(單原子分子氣體)
定壓莫耳比熱
自由度(Degrees of freedom)與莫耳比熱:
能量均分(equipartition of energy)原理:
每一種分子都有 f 個獨立方式去儲存能量,稱為有 f 個自由度。而每一種自由度,相當於每個分子儲存 的能量(或是說每莫耳分子有
能量)。
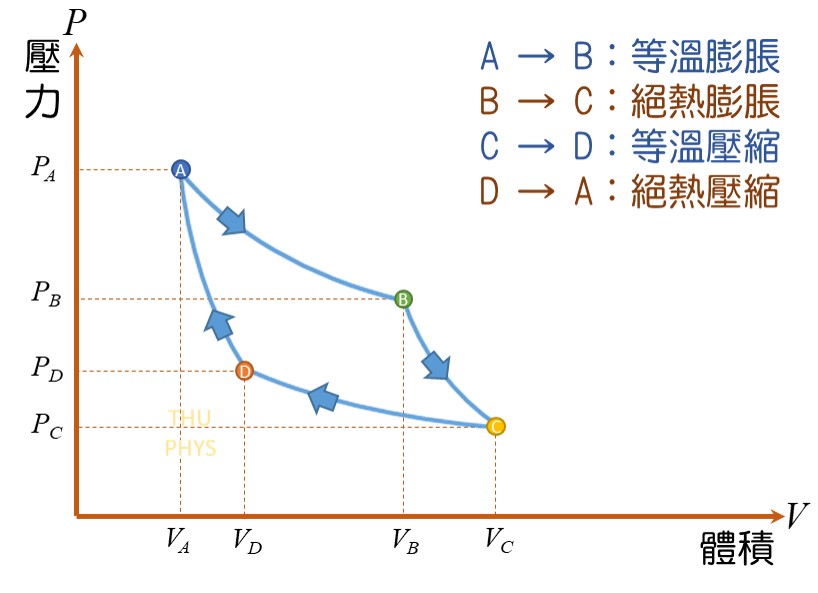
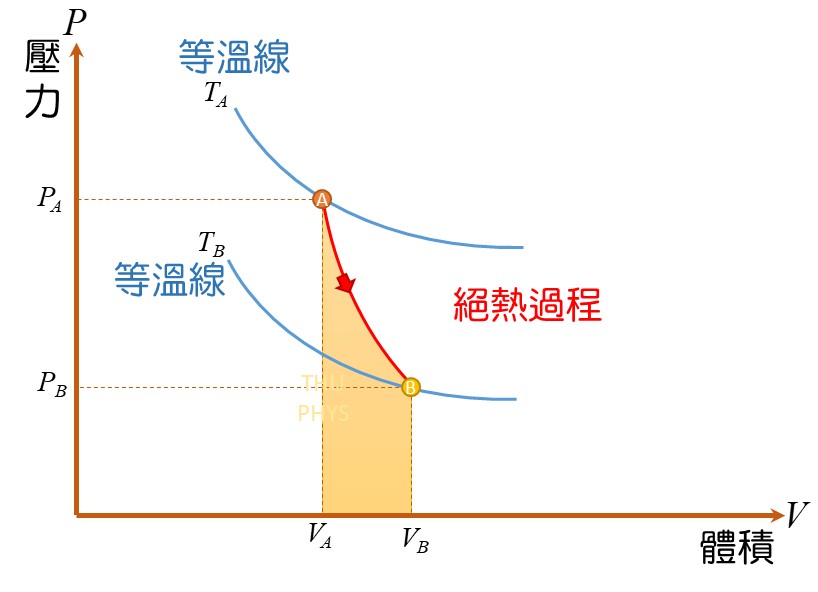
理想氣體(ideal gas)的絕熱膨脹(adiabatic expansion):
理想氣體(ideal gas)自由膨脹( Free expansions):
理想氣體在進行絕熱自由膨脹的過程中,雖然壓力改變了體積也改變了,我們發現溫度並沒有任何變化。
但是對於一般的真實氣體,進行絕熱自由膨脹的時候溫度會下降。
一些整理:
1)孤立系統(isolated system)
一個『完全不與外界交換能量或質量』的系統。任何能量或質量都不能進入或者離開一個孤立系統,只能在系統內移動。
and
or
孤立系統的內能固定。
2)等溫過程(isothermal process)

所做的功,等於等溫線底下的面積。

3)等壓過程(constant-pressure processes)

4)定容過程(constant-volume processes)
系統體積保持一定,因此系統作功為 0,即W = 0。
加熱到系統,則系統內能增加。系統釋放熱,則內能減少。

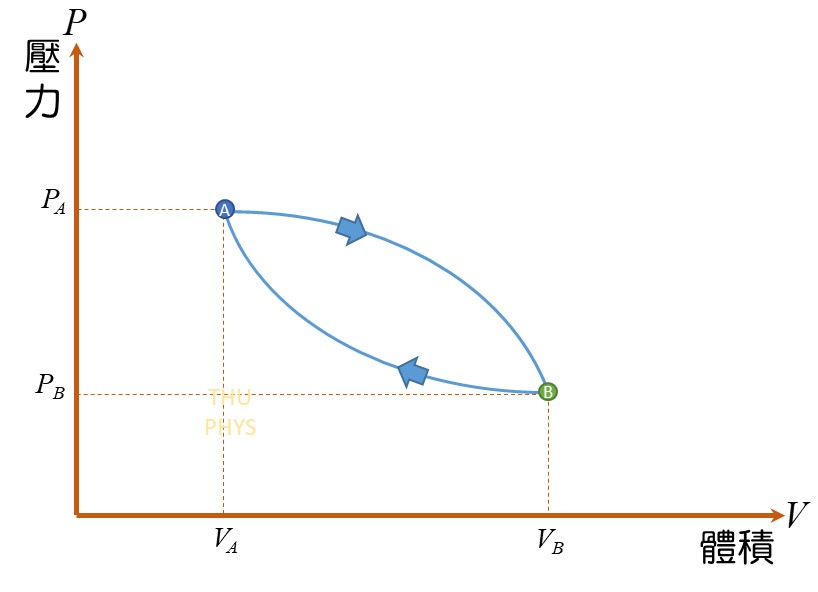
5)循環過程(cyclical processes)
系統經過一連串的變化,回到原狀態,此過程稱為循環過程。
因為系統回到原狀態,因此
6)絕熱過程(adiabatic processes)
系統與環境間完全絕熱。因為絕熱(Q = 0),熱無法進出系統,因此,系統與環境間的關係只有作功。若系統作正功,內能減少。系統作負功(作功於系統上),內能增加。
7)自由膨脹過程(Free expansion processes)
在這個過程中,系統不僅絕熱,而且不作功。也就是 。
氣體動力論所達成的重要結論
=> 氣體分子並非全都有相同的速度,速度的分佈呈現Maxwell-Boltzmann分佈函數,氣體分子的運動平均速率決定於氣體分子的質量和整體系統的溫度。
=> 理想氣體分子的平均動能與氣體的種類和質量無關,只與溫度成正比。
=> 對理想氣體的內能而言,因為氣體分子間沒有交互作用就沒有位能的貢獻,因此氣體分子的動能就是系統的總體能量也就是理想氣體系統的內能。也就是內能僅為溫度的函數,在絕熱自由膨脹的實驗中驗證了這個結論。