
純量(Scalars)與向量(Vectors)
1 】路徑長(Distance):點A到點B間的路徑長,此為純量,圖1中,以紅色虛線表示。
2 】位移(Displacement):兩點位置的改變,此為向量,圖1中,以藍色實線表示。
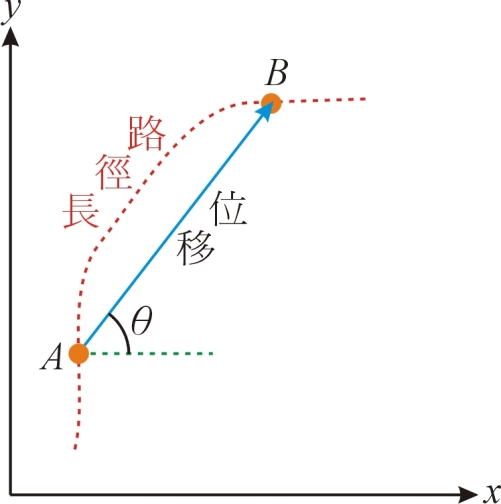 (圖1) |
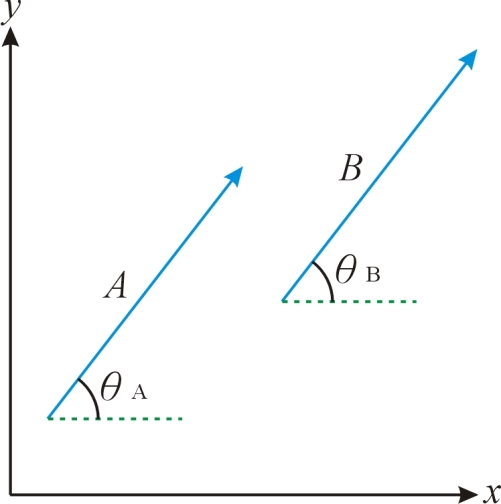 (圖2) |
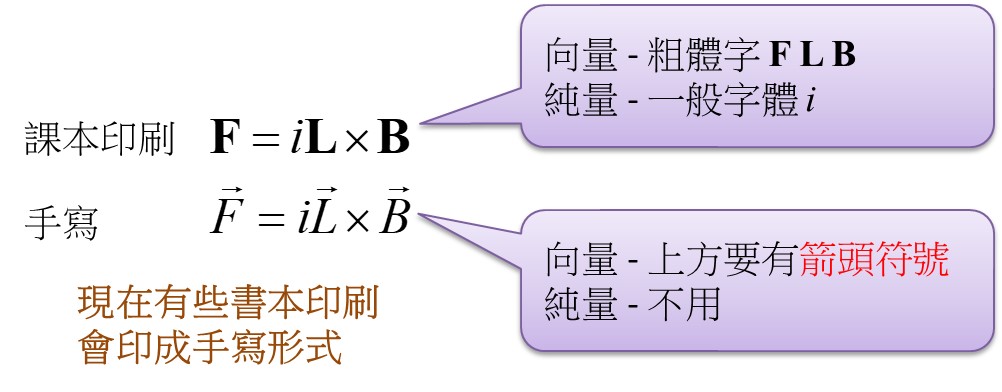
3 】純量:只有大小的量,以「」表示。
4 】向量:有大小,有方向的量,以「」表示。書本印刷體記號為「
」。向量
的大小表示為
或
。
分量:
一個向量 在 xy 平面上,可以將其分為在 x 軸與 y 軸上的兩個分量。
與x軸夾角:
單位向量(Unit Vector):、
、
向量運算:
1】向量加法:向量和
2】純量乘積(內積)(Dot Product):
兩向量 和
,其內積定義為
3】向量乘積(外積)(Cross Product):
兩向量 和
,其外積定義為
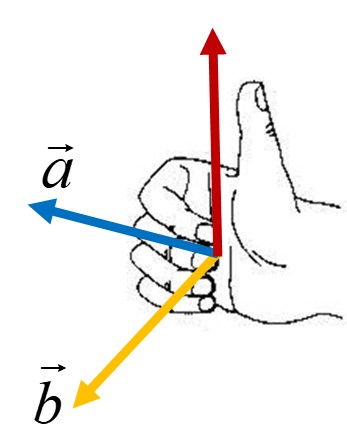
右手定則(right-hand rule):將右手四指由 方向轉到
方向,此時大拇指方向指向
方向。
(※安培右手定則:右手四指方向順著電流方向時,大拇指會指向磁場方向。)
關於行列式展開:
二維行列式定義:
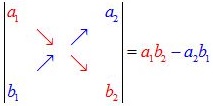
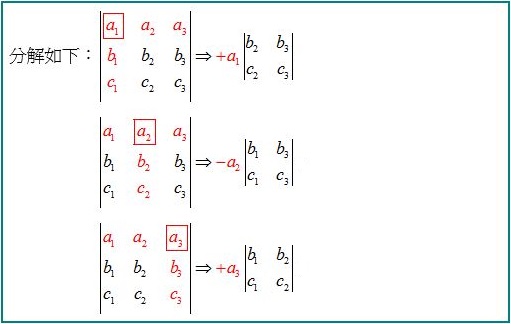
三維行列式可以用二維行列式來表示:
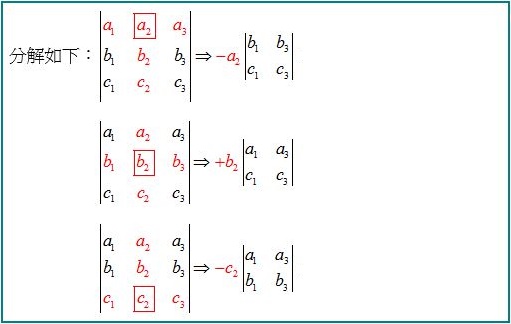
它也可以沿著任何其他的行或列擴展。例如,下列式子是沿著第二行(式子中紅色部分)擴展
另外一種行列式展開的方法:
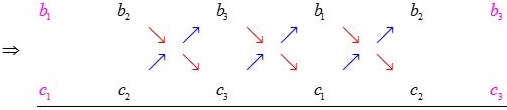
向量外積
梯度(Gradient)、散度(Divergence)與旋度(curl):
3】旋度(curl)
座標系:
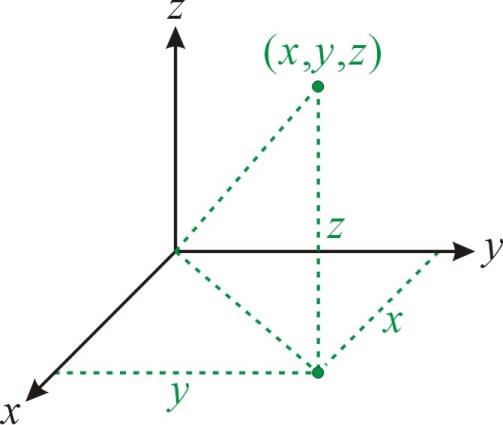
1】直角座標(Cartesian coordinates):
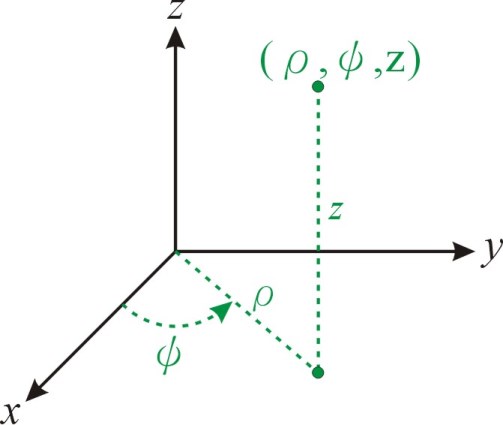
2】柱坐標(Cylindrical coordinates):
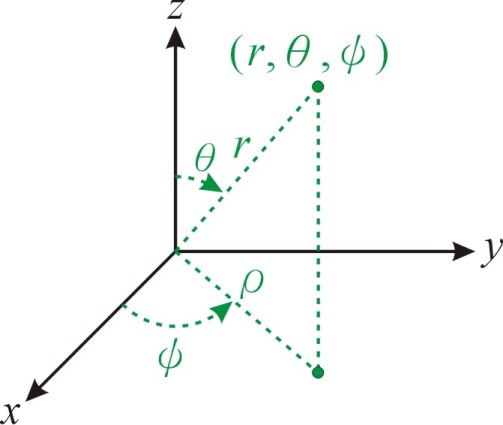
3】球坐標(Spherical Polar coordinates):
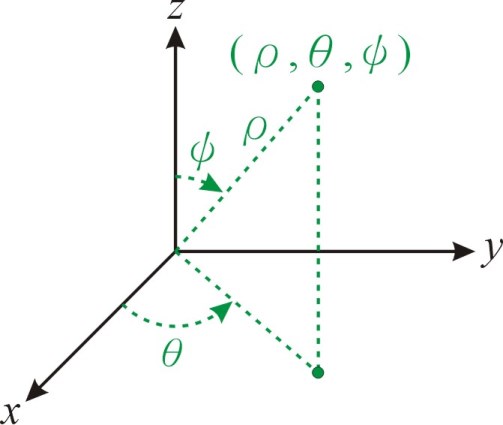
【補充】微積分書本常用定義 等定義,有時與物理書本常用的極座標定義有差異。
補充:三角函數
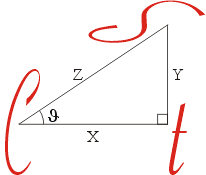
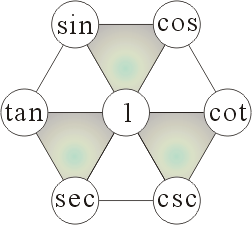
倒數關係:
| |
|
| |
|
| |
平方關係:三個倒三角形(圖中有塗顏色的那三個)

商數關係:逆時針轉一圈
| |
|
|
餘角關係:
提醒:
但
兩角和、兩角差:
和差化積、積化和差:
| |
|
| |
|
| |
|
| |
三角函數的微分: