
熵(Entropy)
最低能量、最大亂度
在一封閉系統發生不可逆過程,系統的【熵】只會增加,不會減少。
熱二的幾種等效表述:
(a)熱量只能從高溫的物體自發地流向低溫的物體,而不可能從低溫的物體自發地流向高溫的物體。
熱量自發地從『高溫』-->--『低溫』(OK)
熱量自發地從『低溫』-->--『高溫』(NO...不可能發生~)
(b)沒有100%效率的熱機 --- 也就是說,將一定量的熱量完全轉化為功...(NO~)。
不可能從單一熱源吸收能量,使之完全變為有用功而不產生其他影響。
(c)自然過程傾向於走向更大的無序狀態或更大的熵。
熵的變化:
在等溫過程中,熵的變化可寫成
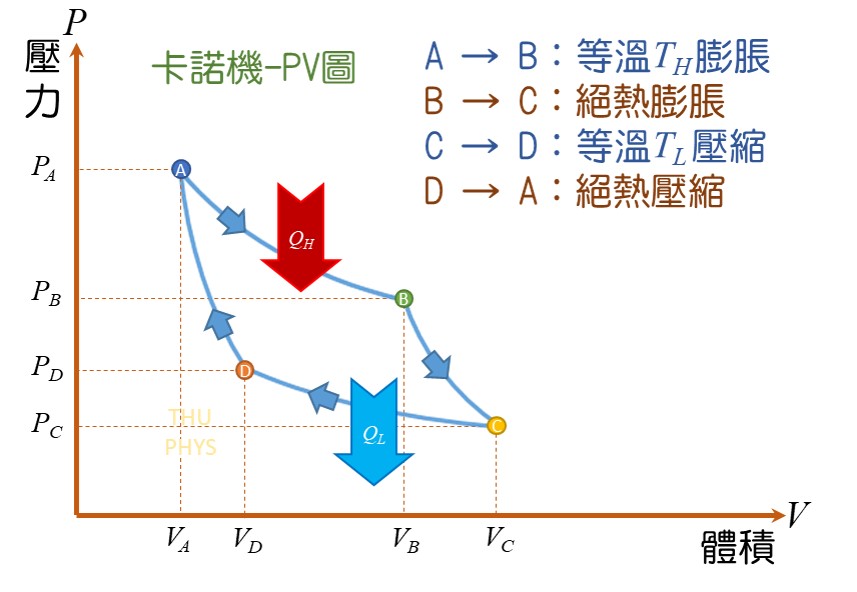
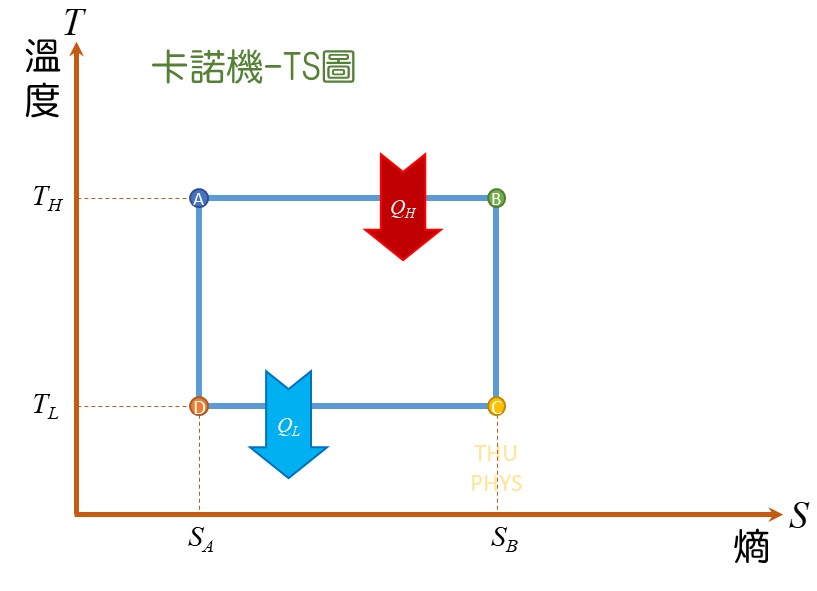
Carnot engine(卡諾機)
卡諾循環:一個假設的可逆循環~
A => B,等溫()膨脹,系統從環境中吸收熱量
。
B => C,絕熱膨脹,系統對環境中作功
C => D,等溫()壓縮,系統向環境中放出熱量
。
D => A,絕熱壓縮,環境對系統作功 ,系統恢復原來的狀態。
其中
==> 將熱能()完全轉換為機械能(
)~
A => B:......(1)
B => C:
......(2)
C => D:......(3)
D => A:......(4)
(2)、(4):
(1)、(3):
Carnot efficiency(卡諾效率...thermal efficiency,熱效率)
熱效率只取決於溫度,熱機效率永遠小於1,也就是說,熱機在無外力幫助下,是無法將來自高溫獲得的『熱』(Q),完全轉換成有用的『功』(W)。
依卡諾循環設計的引擎,稱為卡諾熱機(Carnot heat engine)。
將卡諾循環反向進行:卡諾冷機(Carnot refrigerator),A => D => C => B => A。系統自低溫吸取熱量 ,向高溫輸送
,外界對系統做功。
效能係數(coefficient of performance, COP):
====================
熱機-引擎
冷機-冰箱、暖氣機
卡諾循環是理想的假設狀態。
Stirling Engine(史特靈機)
熱力學
第 0 定律】熱平衡,溫度一樣。
第 1 定律】,能量守恆。
第 2 定律】,系統的熵不會減少。
第 3 定律】不可能達到『絕對零度』。